Lecture 1 (Autoregressive Models)

Likelihood-based models

• Problems we’d like to solve: Generating data, compressing data, anomaly detection
• Likelihood-based models estimate the data distribution from some samples from the data distribution
• the aim is to estimate the distribution of complex, high-dimensional data with computational and statistical efficiency.

Generative models

• Maximum likelihood: given a dataset x(1), …, x(n), find θ by solving the optimization problem.

  

• It is equivalent to minimizing KL divergence between the empirical distribution and the model.

  

  How do we solve this optimization problem?

  • Stochastic Gradient descent

  Why maximum likelihood + SGD? It works with large datasets and is compatible with neural networks.

Designing The Model

• The key requirement for maximum likelihood + SGD: efficiently compute log p(x) and its gradient.
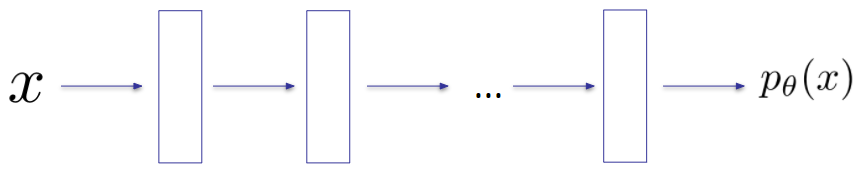
• pθ —> deep neural network

Autoregressive model

An expressive Bayes net structure with neural network conditional distributions yields an expressive model for p(x) with tractable maximum likelihood training.

RNN autoregressive models - char-rnn

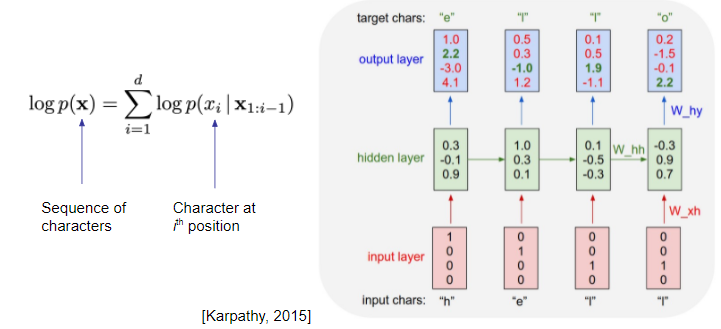
Masking-based autoregressive models

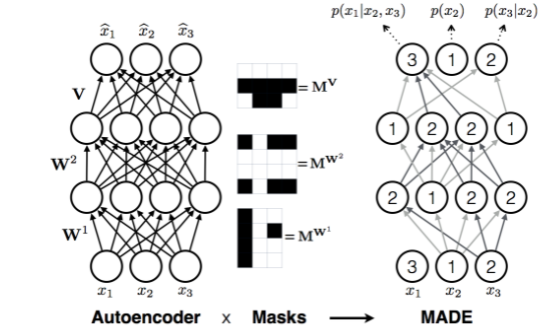
• Masked Autoencoder for Distribution Estimation (MADE)

  

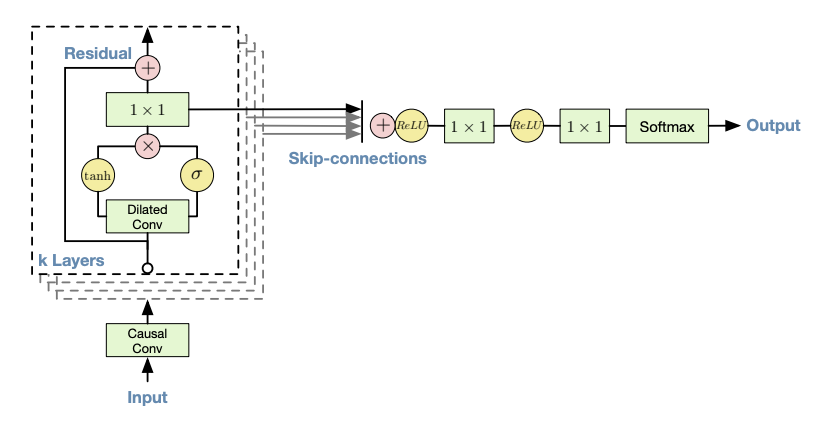
Masked Temporal (1D) Convolution (WaveNet)

Improved receptive field: dilated convolution, with exponential dilation. Better expressivity: Gated Residual blocks, Skip connections.

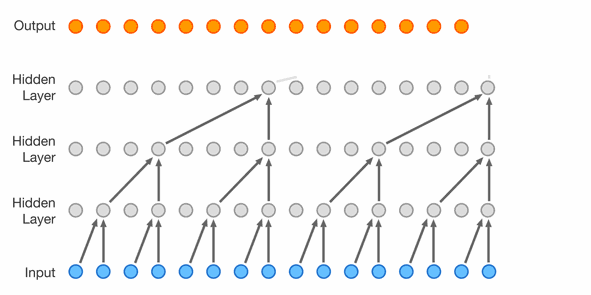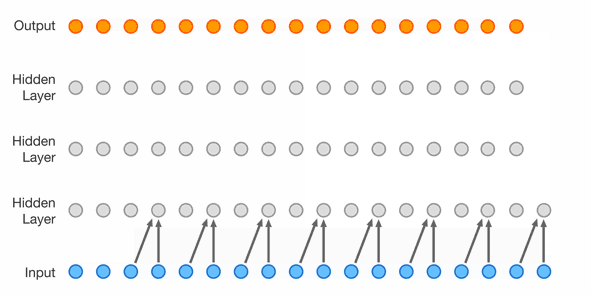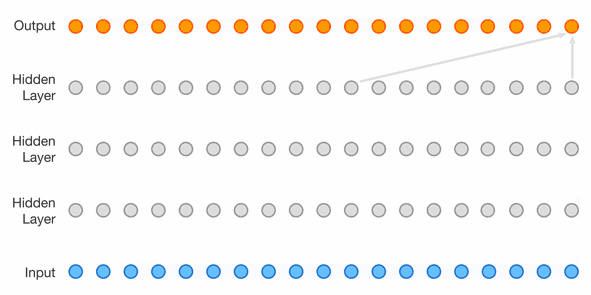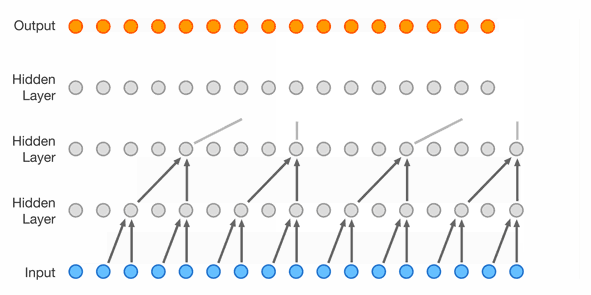
Masked Spatial (2D) Convolution - PixelCNN

• Images can be flatten into 1D vectors, but they are fundamentally 2D.
• We can use a masked variant of ConvNet to exploit this knowledge.
• First, we impose an autoregressive ordering on 2D images:

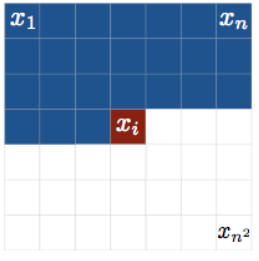
PixelCNN

PixelCNN-style masking has one problem: blind spot in the receptive field.

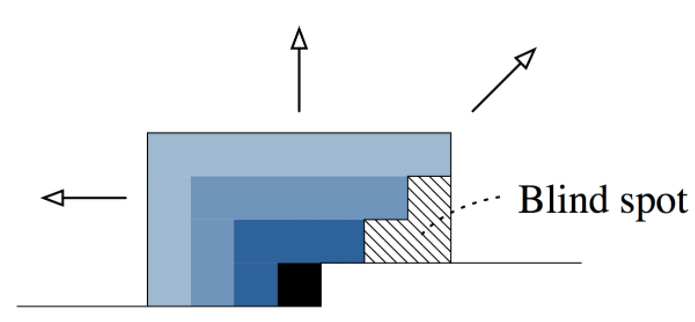
Masked Attention + Convolution

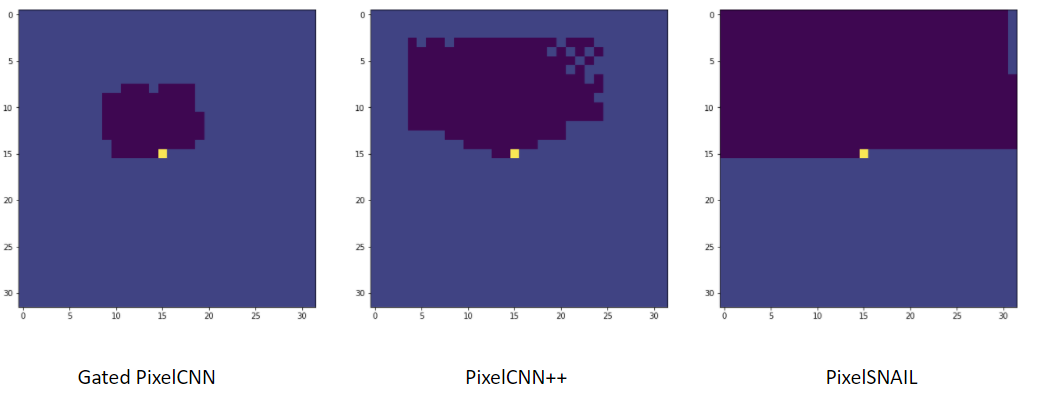
Neural autoregressive models: the good

Best in class modeling performance:

• expressivity - autoregressive factorization is general.
• generalization - meaningful parameter sharing has good inductive bias.

Masked autoregressive models: the bad

• Sampling each pixel (1 forward pass)

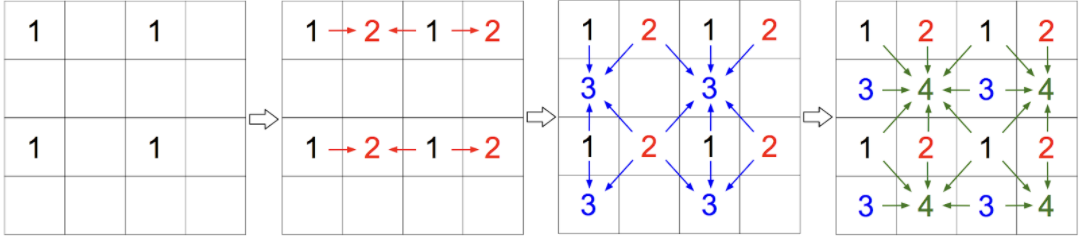
  Speedup by breaking the autoregressive pattern

  • O(d) -> O(log(d)) by parallelizing within groups {2, 3, 4}.
  • Cannot capture dependencies within each group: this is a fine assumption if all pixels in one group are conditionally independent.
    • Most often they are not, then you trade expressivity for sampling speed.

  

Natural Image Manipulation for Autoregressive Models using Fisher Scores

• Main challenge:
  • How to get a latent representation from PixelCNN?
  • Why hard? The random input happens on a per-pixel sample basis.
• Proposed solution
  • Use Fisher score

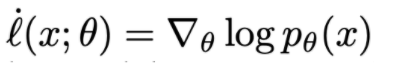
Lecture 2 (Flow Models)

• How to fit a density $p_Q(x)$ model with continuous $x \in R^n$
• What do we want from this model?
  • Good fit to the training data (really, the underlying distribution!)
  • For new x, the ability to evaluate $p_\theta (x)$
  • Ability to sample from $p_\theta (x)$
  • And, ideally, a latent representation that’s meaningful

How to fit a density model?

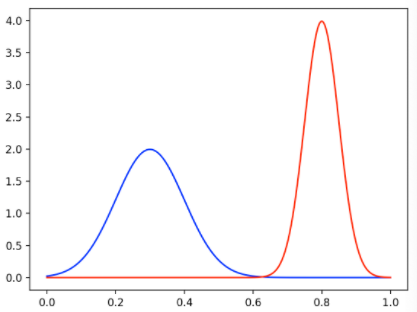
Option 1: Mixture of Gaussians

Parameters: means and variances of components, mixture weights

Option 2: General Density Model

• How to ensure proper distribution?

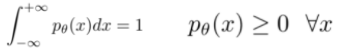
• How to sample?
• Latent representation?

Flows: Main Idea

Flows: Training

Change of Variable

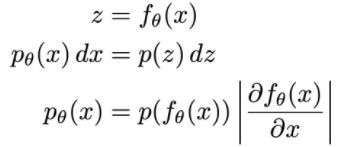
Note: requires invertible & differentiable

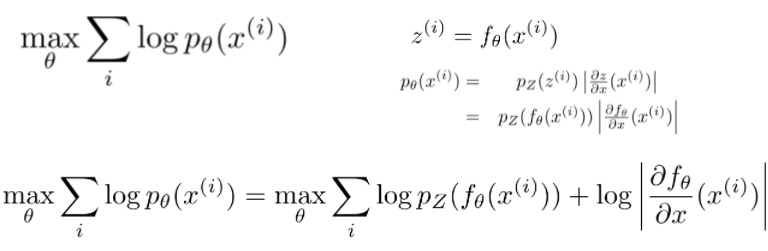
assuming we have an expression for , this can be optimized with Stochastic Gradient Descent

Flows: Sampling

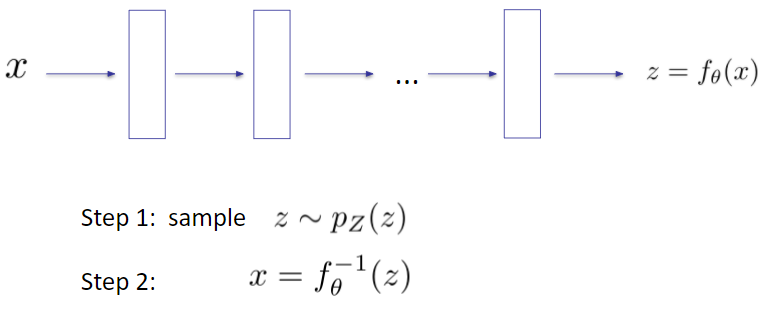
2-D Autoregressive Flow

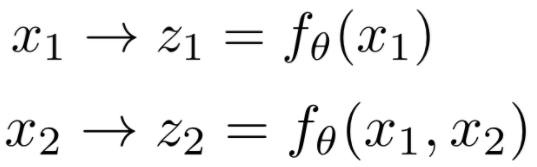
2-D Autoregressive Flow: Face

Architecture: Base distribution: Uniform[0,1]^2 x1: mixture of 5 Gaussians x2: mixture of 5 Gaussians, conditioned on x1

Autoregressive flows

• How to fit autoregressive flows?

  • Map x to z
  • Fully parallelizable

• Notice

  • x → z has the same structure as the log likelihood computation of an autoregressive model
  • z → x has the same structure as the sampling procedure of an autoregressive model

  

Inverse autoregressive flows

• The inverse of an autoregressive flow is also a flow, called the inverse autoregressive flow (IAF)
• x → z has the same structure as the sampling in an autoregressive model
• z → x has the same structure as log likelihood computation of an autoregressive model. So, IAF sampling is fast

AF vs IAF

• Autoregressive flow
  • Fast evaluation of p(x) for arbitrary x
  • Slow sampling
• Inverse autoregressive flow
  • Slow evaluation of p(x) for arbitrary x, so training directly by maximum likelihood is slow.
  • Fast sampling
  • Fast evaluation of p(x) if x is a sample
• There are models (Parallel WaveNet, IAF-VAE) that exploit IAF’s fast sampling.

Change of MANY variables

For , the sampling process f-1 linearly transforms a small cube to a small parallelepiped . Probability is conserved:

Intuition: x is likely if it maps to a “large” region in z space

High- Dimensional Flow models: training

Change-of-variables formula lets us compute the density over x:

Train with maximum likelihood:

New key requirement: the Jacobian determinant must be easy to calculate and differentiate!

NICE/RealNVP

• Split variables in half:

• Invertible! Note that $sθ$ and $t_θ$ can be arbitrary neural nets with no restrictions.
  • Think of them as data-parameterized elementwise flows.